How not to teach music

I spent a good deal of my procrastination time yesterday searching for some interesting serious music blogs to put on my link list. To my dismay, there seem to be surprisingly few--of the sort I am looking for, at any rate. Well, I suppose I can try to do my part to fill this niche (albeit very gradually...)

The blog of the Texas Tech University music theory faculty is among the most suitable that I found. They certainly have at least one thing going for them: a picture of Heinrich Schenker on their profile! Sadly, however, I did not have to look very far to confirm what I already knew very well: at Texas Tech, just like pretty much everywhere else, the lessons of Schenker's work have yet to reach the place where they are most desperately needed--namely, the teaching of music to beginning students (say, at the freshman level).

This may sound controversial to some, so let me ease into the point somewhat gradually. Consider the end of this post about a couple of famous moments in Beethoven's symphonies:

P.S. to undergraduate harmony students: If you write a tonic chord and dominant
chord simultaneously, I will mark it wrong. :)

To be sure, this is a lighthearted remark, as the smiley makes clear. But somehow I don't think the author of the post is lying: he or she undoubtedly will mark you wrong if you write a passage like the one Beethoven wrote. Question: why, exactly? The obvious answer is that writing such a thing would necessarily involve violating the directions of whatever exercise the student was doing. But if that's the case, why would a student even be tempted to write a simultaneity of the type in question? Consider this analogy: suppose a calculus student is asked on an exam to evaluate the integral of x^2 from 0 to 1, but instead of doing so, writes down a proof of Stokes' Theorem. Well, yes, I suppose the student would techincally have to lose points for not actually answering the question; but not before they were pulled aside and asked "why aren't you in a higher course?" This kind of thing is of course very unlikely to occur in practice (except perhaps as a prank at elite schools), for good reason: everyone, including students, knows that if you understand the concepts involved in Stokes' Theorem, you don't belong in first-year calculus, so such students don't typically wind up in such courses.

What's the difference in music? Are students of Beethovenian musical genius being made to sit through courses below their level, while being admonished to keep their advanced knowledge hidden from view? Well, it's possible, I have to admit. But the hypothesis that the students being marked wrong are geniuses turning in great music in place of simple exercises, is, I think, quite a bit less plausible than the hypothesis that I favor, namely that they are the victims of unsystematic instruction who simply ran astray during the obligatory regurgitation process. Simply put, a tonic-dominant clash (for example) is not treated by the curriculum as an advanced phenomenon, beyond the conceptual grasp of beginning students; it's treated as a forbidden phenomenon that, after paying your dues, you may be allowed to sample later in life, under appropriate circumstances--much like alcohol.

It would be like teaching calculus by first showing the students the course textbook, and saying "imitate the 17th and 18th century mathematics that you find in here"; and then showing them passages from several more advanced mathematics books and saying "do not write what you find in here--these are developments of the 19th century and beyond, outside of the 'common practice period' of Western mathematics." (You can even imagine a student's objection: "but look at this ingenious proof of Euler's which steps outside of 'common practice' and seems far ahead of its time." And the teacher's reply: "When you are an Euler, you can write that way; but if you use such ideas in this course, I will mark you wrong.")

If we taught mathematics this way--sample passages from books, with elementary passages labelled "do" and advanced passages labelled "don't"--you can easily imagine that students would not only have difficulty remembering how to reproduce elementary passages, but they would mix them up with the "forbidden" advanced passages! Actually, to a certain extent, we do unfortunately teach elementary mathematics in terms of (seemingly arbitrary) "rules" to be followed--and to exactly that extent, we frequently (and predictably) get back nonsense on tests. To be sure, some bright students can figure things out for themselves and thus survive this kind of instruction with their (mathematical or musical) reasoning ability intact, but the rest are lost.

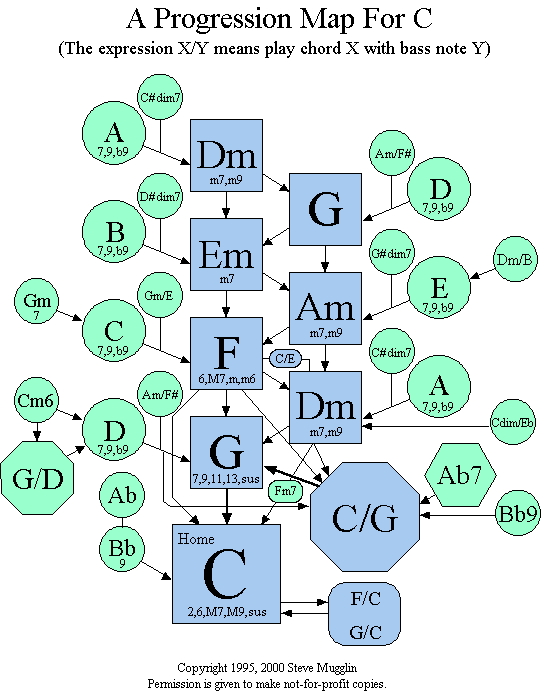
Is this analogy unfair? Am I being too harsh? Well, I certainly don't mean to pick on the Texas Tech faculty in particular; they are just like (and possibly better than) everybody else. But they have a blog, so they have opened themselves to serving as my foil! So let's consider this post of theirs having to do with "some basic rules of harmonic progression" (a phrase that already makes me wince). At least they don't endorse that awful diagram that they (and I, at the top of this post) have reproduced. (It reminds me of Piston's infamous "I is followed by IV or V, sometimes VI...", except it's even worse.) To their credit, the Texas Tech theorists manage to reduce the number of letters to three:

Now, throw away your chart. Here's all you need to know. To create an effective
harmonic progression in the common practice style, you can string together the
letters T, P, and D in any order provided that a P never follows a D. All of
these will make coherent harmonic progressions:T-P-D-T (could be realized as
I-ii-V-I)T-T-P-D-T (could be realized as I-I6-IV-V-vi)T-T-T-T-T-T (could be
realized as I-I6-I-vi-vi6-I)T-D-D-T (could be realized as I-vii-V-I)...and so
on. Once you come up with a string of Ts, Ps, and Ds, simply substitute a chord
with the corresponding function into your string. Then all you need to do is
follow the rules of partwriting and you should be well on your way to successful theory homework.

Ah, yes, successful theory homework (maybe even a grade of "A")--could there be any loftier goal? Seriously, my purpose isn't to sneer at the good folks of the Texas Tech music department. Actually, on its own terms, the simple formalism they describe has a certain appeal, especially since they emphasize its combinatorial nature: the letters may be combined in any way whatsoever, subject only to the one caveat mentioned. But I have a question: why is there a caveat at all? We're talking about (classes of) sequences of pitch-class collections here--a rather abstract level of musical description, embracing quite a large number of different concrete realizations. Who dictated from on high that no "P" shall ever follow a "D"? What was the original definition of "effective harmonic progression in the common practice style" that was used to derive this result? And, however it is defined, why is this class of "effective progressions" one that anyone should care about?

The point is that "chord progressions" are not the building-blocks of music. If they have any legitimate role in the analysis of music at all (a notion of which I am quite skeptical), it is as a highly specific (if abstract) type of emergent motivic phenomenon that applies in particular works. But that's not how they are used in freshman theory. In freshman theory, they are presented as a way of describing (statistically, as it were) the events typically encountered on the musical surfaces of works of a certain historical period. To call this pedagogically unsound would be an understatement; it is downright atrocious. Leave aside the question of how effective this vocabulary is for the purpose of statistical description; the important point is that while wasting their time with these descriptions, the students do not learn (or learn very poorly) the conceptual processes that produce these musical results.

Conceptual processes are the ingredients of music. They are what actually occupy the minds of composers and performers when practicing their art. The actual notes of a piece are the results of these processes, and are thus are in some sense incidental by-products. Let me illustrate with the Beethoven examples quoted by the Texas Tech theorists (click to enlarge):

In neither of these cases is the underlying process "simultaneous sounding of the tonic and dominant chords". The underlying processes are, rather, the much more fundamental ones of "anticipation" and "delay". In the first example, the famous "premature" horn entrance from the Eroica, the horn anticipates the arrival of E-flat at the beginning of the recapitulation. The result produced is not an entity called "tonic-on-top-of-dominant-chord"; rather, the horn, in its eagerness to get to E-flat, simply doesn't care what notes are being sounded in the strings at the same time. It's nothing but an elaborate version of a traditional "nonharmonic tone" (a term we really need to get rid of).

The second example, from the Fifth Symphony, is somewhat more complex, but equally illustrative, this time of the use of delay. The scherzo was supposed to have ended at m. 324, but the cellos and basses refused to cooperate: instead of proceding from G up to C, they insisted on prolonging the G (by sliding it up to neighboring A-flat, then down through itself to F-sharp, and back). By the time we reach the beginning of the quoted passage (m.348), the first violins have added to the tension by "defecting" and lending contrapuntal support to the mutinous G. (Incidentally, I disagree with the TTU theorist's analysis of the passage: in my opinion, the span pitch in the top voice between m. 351 and m. 355 is D, not E-flat.) They proceed to hurriedly climb up the scale (once again, I am not sure I am comfortable with TTU's assignment of superordinate status to the G, B, and D of this climb), at the top of which they are joined by the rest of the orchestra save the timpani and bassoons, whose loyalty to C remains unrelenting. Finally the orchestra can hold its breath no longer, and releases the long-suppressed C, and with it the fourth movement, in a giant ejaculatory burst.

Do not be fooled by the narrative style of the preceding paragraphs: they represent very specific parsings of the notes involved in the passages. There is, in fact, a notational system, devised (or, more accurately, suggested) by Schenker, by means of which the above analyses could be formally expressed. (Schenker of course was also quite proficient in the art of running verbal commentary, which he regularly used even in his later work, in combination with his "graphs".) I might even have made use of it here, if I had the patience to do the necessary fiddling with LilyPond.

Now I ask you: what does the idea of "chord progression" add to our understanding of either of these passages? Are the notes (and thus the "chords") of the score not the inevitable result of procedures such as described above (anticipation, delay, or prolongation via passing motion/neighbor embellishment)? Take another look at the above musical examples, and try to explain to me what additional musical information is conveyed by the notations at the bottom. Seriously--I want to know.

And what about those question marks? Do they mean that the analyst is clueless about the functions of the notes in "question"? I certainly hope not. What they evidently mean is that the particular simultaneity they refer to does not have its own name. But why should it? Why should every possible coincidence of musical events have a name? ( I am reminded of one of the more absurd episodes of musical history, namely when Schoenberg's Verklärte Nacht was rejected for performance on the grounds that it "contained a chord which could not be found in any book".) Music, after all, is like language in that it makes infinite use of finite means; and it is those finite means, not particular uses of them, with which music theory must be principally concerned.

If music students were given systematic instruction in the processes, or operations, by which notes are generated, rather than a loosely organized taxonomy of particular note successions that happen to be common, then their homework assignments would make a lot more sense--both to them and to their instructors. Exercises would be constructive, rather than restrictive, in nature--so that students would not have to be explicitly told to avoid "wrong" (i.e. complex) constructions; the latter would simply not occur to them in the first place until they had the tools to produce them. We could at long last dispense with the unhelpful and unhealthy idea that Beethoven (or Schoenberg, or whoever) "broke the rules" or "took liberties"-- recognizing instead that the "revolutionary" contributions of such composers consisted only in taking the procedures of their predecessors to higher levels of complexity. (A corollary to this would be the disappearance of useless categorial distinctions such as "tonal/atonal".) Best of all, one could study music theory and music itself simultaneously (and maybe, Godwilling, the distinction would go away, as Schenker fervently wished).